**********************************************************

Introduction to Special Relativity

　　　特殊相対性理論の紹介

**********************************************************

　　　萩原良昭の著書の補足資料( Appendix_3-1-2 ) です。

**********************************************************


**********************************************

　　　　 人工知能パートナー（ＡＩＰＳ）を支える　　　

　　　 　　　デジタル回路の世界

　　　　
***************************************　　

ISBN 978-4-88359-339-2 C3055

本体 9000円＋税　

Ｂ５サイズ　上製　475ページ　（ハードカバー）

***************************************


　 書籍の出版社の紹介　　

　TEL: 042-765-6460(代) 　　青山社

https://www.seizansha.co.jp/ISBN/ISBN978-4-88359-339-2.html


***************************************




＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　　　　　　　　　　　　　　Appendix 3-1-2 　
　　　　　
　　　　　　　　　　　　　 Field Tensor F[ ][ ] と　Maxwell　の方程式

　 　　　　　本書　「デジタル回路の世界」の　(pp.182～192)　　の補足資料です。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


　　　　　　　　　　　　　　　 特殊相対性理論

　　　　　
　　　　　　　　　　　 ものごとは見る立場によって違って見えます。
　　
　　　　　　　　　　同じものと思っていても実は違って見える場合があります。

　　　　　　　　　 しかし、まわりの人は動いていても、自分の立場から見ると、
　
　　　　　　　　　自分自身はいつも自分の世界の中心にいて静止しています。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊










＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　　　　　（１）座標系の定義

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

宇宙の中心はどこにあるのでしょうか？
　あなたの見る宇宙の中心はあなた自身です。
　　　　 あなたは宇宙の中心にいます。

自分自身の固有の時空間の中心で生きています。
　　　　　　世界中の人、一人ひとりが
　　　　このすばらしい宇宙の中心にいます。

自分自身の固有の時空間の中心で生きています。


まず、座標系の定義から始めます。




＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

(A) 観察者Ａの座標系


まず、観察者Ａの座標系の定義です。

観察者Ａの座標系の原点を０とします。

観察者Ａの座標系のＸ軸を観測者Ａの前方に取ります。

観察者Ａの座標系のＹ軸を左手方向に取ります。

観察者Ａの座標系のZ軸を頭上方向に取ります。

さらに観察者 Ａ の固有時間 ｔ を含ませると Ａ の座標系は Ａ( x, y, z , t ) となります。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊




(B) 観察者Bの座標系


観察者Ｂの座標系の原点をＯ’とします。

観察者ＢのＸ’軸を観測者Ｂの前方方向に取ります。

ここで観察者ＡのX軸座標とＢのX’軸座標の間で
　
次の線形関係式が成り立つとします。

X’ = α X + β t　　 ... (1) とします。

観察者ＢのＹ’軸を観測者Ｂの左手方向に取ります。

Y’ = - Y 　　　　　　　 ... (2) となります。

観察者ＢのＺ’軸を観測者Ｂの頭上方向に取ります。

Z’ = Z 　　 ... (3) となります。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　観察者 A の座標系の定義

X 軸（前方）
Y 軸（左手）
Z 軸（頭上）

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　観察者 B の座標系の定義

X’ 軸（前方）
Y’ 軸（左手）
Z’ 軸（頭上）

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　さらに観察者 Ｂ の固有時間 ｔ’ を含ませると

　Ｂの座標系はＢ( x’ , y’, z’ , t’ ) となります。

　ここで、時計の進む速さは観察者によって違うとします。

　観察者ＡとＢの固有時刻 t と t’ の間で

　次の線形関係式が成り立つとします。


　　　　　　t’ = γ X + δ t ... (4)


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

X’ = α X + β t ... (1)

Y’ = - Y ... (2)

Z’ = Z ... (3)

t’ = γ X + δ t ... (4)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


次に２つの座標系の同等性について考察を続けます。


　Ａにとっての、自分の固有時間 ｔ を含んだＡ( x , y, z , t ) 座標系の形と、
　
　Ｂにとっての、自分の固有時間 ｔ’ を含んだＢ( x’ , y’, z’ , t’ ) 座標系の形は、
　　　　　
まったく同じ形をしているとします。

これを　「２つの座標系は同等である」　と言います。


２つの座標系は、同等・同一で対称的です。

２つの座標系の変換式は、同じ物理定数で、

同じ形式で、記述することができるはずです。

これを座標系の相対性といいます。




＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
Aの座標系( t, X, Y, Z) から見たBの座標系( t', X', Y', Z')
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

X’ = α X + β t ... (1)

Y’ = - Y ... (2)

Z’ = Z ... (3)

t’ = γ X + δ t ... (4)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
Bの座標系( t', X', Y', Z') から見たAの座標系( t, X, Y, Z)
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

X = α X' + β t' ... (5)

Y = - Y' ... (6)

Z = Z' ... (7)

t = γ X' + δ t' ... (8)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊








＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　（2）光の速度 C は不変（普遍）～約３億m/sec～約30万Km/sec


　　　Ｃ = 299792458 m/sec

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊






＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


　　　　　座標系の相対性と光の速度の不変（普遍）性から、

　　　　後は高校数学でLorentz 変換式を導くことができます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　　　　　　　　　Ｌｏｒｅｎｔｚ　変換式

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

X’ = α ( X - v t ) ... (9)

Y' = - Y ... (10)

Z' = Z ... (11)

t’ = α ( v X / c | 2 - t ) ... (12)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

X = α ( X' - v t' ) ... (13)

Y = - Y' ... (14)

Z = Z' ... (15)

t = α ( v X' / c | 2 - t' ) ... (16)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件③： α = - 1 / sqrt ( 1 - ( v/c ) | 2 ) ... (17)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

変換式の対称性からの考察 Step(1) :


X’ = α X + β t　= α ( α X’ + β t’ ) + β ( γ X’ + δ t’)

= ( α | 2 + β γ ) X’ + ( α β + β δ ) t’


t’ = γ X + δ t　= γ ( α X’ + β t’ ) + δ ( γ X’ + δ t’ )

= ( γ α + δ γ ) X’ + ( γ β + δ| 2 ) t’



変換式の対称性からの考察 Step(2) :



( α| 2 + β γ ) = 1 ; ( α β + β δ ) = 0 ;

( γ α + δ γ ) = 0 ; ( γ β + δ| 2 ) = 1 ;


変換式の対称性からの考察 Step(3) :



＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件①　：　δ = - α 　; γ = ( 1 - α | 2 ) / β ;

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


初期状態　t = t’ = 0　の時 の考察


初期時刻 　( t = t’ = 0 )　には　A と B の原点 O と O’ は　同じ位置 にあるとします。

すなわち、時刻が t = t’ = 0 の時、位置が X = X’ = 0 とします。

その後、お互いから遠ざかる場合を考えます。


事象（Ａ）の定義（観察者BがAの動きを観察する場合）

事象（Ａ）の定義とは、単純にＡ の場所と時間におきる出来事や現象のことです。

観察者B から見て、A は、B のX’軸正の方向に速度 V で遠ざかるとします。

A の原点 Ｏ の座標値　X=0 は、B の座標系では　X’ = v t’ に対応します。



Ａの事象( X=0; t=t ) をＢが見ると、 X = 0　; X’ = v t’ となります。

　　　X = α X’ + β t’ 　　；　 t = γ X’ + δ t’　　；

から、　 0 = α v t’ + β t’　を得ます。


したがって、　

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件②： β = - α v　　；　を得ます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊





次に、原点から出た光の事象 (event)＝（その位置と時刻）
　　
　　光は観察者ＡのＸ軸の正の方向に進むとする。

観察者 A から見た 光 の位置 X = c t 　；

観察者 B から見た 光 の位置 X’ = - c t’ ；


X’ = α X + β t　；

　 t’ = γ X + δ t　；


より、次式を得る。

- c t’ = α c t + β t　　；

t’ = γ c t + δ t　；


よって次式を得る。

　　　t’ / t = γ c + δ = - α - β / c　；


　　c ( 1 - α| 2 ) /( - α v ) - α = - α + α v / c ;

- c ( 1 - α | 2 ) / α v = α v / c ;

( 1 - α| 2 ) = - ( α v / c ) | 2 ;

1 = α| 2 ( 1 - ( v / c ) | 2 )


よって次式を得る。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件③： α = - 1 / sqrt ( 1 - ( v/c ) | 2 ) ... (17)

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


条件　①＋②＋③　より、

γ = ( 1 - α| 2 ) / β = ( α| 2 - 1 ) / α v = α ( α - 1 ) / α v = α v / c ;


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件④ ： γ = α v / c | 2 ;

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

条件　①＋②＋④　より、

X’ = α ( X - v t ) ;

t’ = α ( v X / c | 2 - t ) ;


X = α ( X’ - v t’ ) :

t = α ( v X’ / c | 2 - t’ ) ;


これで最終的に　Lorentz 変換式が求まりました。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊







＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　 　　　 （3）時間の進む速さ

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


座標系Ａも座標系Ｂも動いている相手の時間がゆっくり進む様に見える！

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊





＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

座標系Ａから見て、 動いて見える物体Ｂの時間（ｔ’）はゆっくり進みます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


事象Ｂ ( X=vt ; t=t ; ) --> Δt’/Δt = - 1/α　= sqrt( 1 - ( v / c ) | 2 ) < 1 ;


事象Ｂということは観察者はＡの場合である。


車を運転する運転手（Ｂ）からは、自分の固有時間の速さは不変だが、

地上にいる人（Ａ）の固有時間（ｔ）に対して、Ａが見る車（Ｂ）の時計（ｔ’） は

ゆっくり進んでいるように見える。


Ａ から見てＢが動いて見えます。
　
　 Ａ の固有時刻 t に対して、　　Ｂの時刻 ｔ’　は Ａ から見て

　t’ / t = - 1/ α 　= sqrt( 1 - ( v / c ) | 2 ) < 1 ; となり、

Ｂ の時刻 t’ はゆっくり進んでいる ように観察者Ａからは見えます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊





＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

座標系Bから見て、 動いて見える物体Aの時間（ｔ）はゆっくり進みます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


事象A ( X'=vt' ; t'=t'; ) --> Δt/Δt' = - 1/α　= sqrt( 1 - ( v / c ) | 2 ) < 1 ;


事象Aということは観察者はBの場合である。


車を運転する運転手（A）からは、自分の固有時間の速さは不変だが、

地上にいる人（B）の固有時間（ｔ'）に対して、Bが見る車（A）の時計（ｔ） は

ゆっくり進んでいるように見える。


B から見てAが動いて見えます。
　
　 B の固有時刻 t ' に対して、　　Aの時刻 ｔ　は B から見て

　t / t ' = - 1/ α 　= sqrt( 1 - ( v / c ) | 2 ) < 1 ; となり、

A の時刻 t はゆっくり進んでいる ように観察者Bからは見えます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊





＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

事象（Ｃ）の定義

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　
　　　　事象（Ｃ）とは、単純に飛んでゆく光の先端の、

　　　　場所と時間におきる出来事や現象の事とします。


　　　　原点から出た光の事象 (event)＝（その位置と時刻）　：


　　　　　たとえば、次の場合を考えます：


　　　　　　観察者 A から見た 光 の位置 X = c t

　　　　　　観察者 B から見た 光 の位置 X’ = - c t’


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

まず、　次の関係から、

　　　　X’ = α ( X - v t ) :

　　 t’ = α ( v X / c | 2 - t ) ;


次式を得ます：

　　　　- c t’ = α ( c t - v t )　　　　；

　　 t’ = α ( v t / c - t )　　；



事象(C) に関して次の関係を得ます。


　　　　　t'/t = - X'/X = sqrt ( ( c - v ) / ( c + v ) ) < 1 ;


観察者Ａから見て、この光は ( t , X = ct )　に見えるが、

観察者Ｂから見ると、この光は ( t' , X' = - ct' )　に見えることになる。



観察者Ａから見て光が前方に通り過ごして離れていく距離の値Xに対して

観察者Bから見て光が後方に通り過ごして離れていく距離の値X'は短く見える。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊







＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

事象（Ｄ）の定義

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


観察者（Ａ）の座標系で、観察者（Ｄ）は　X = d で静止しているとする。

今、観察者（Ａ）の座標系で、　ｔ＝0 の時、光が原点からＸ軸正の方向に

出てとする。　X = d = ct ; t = d/c で　光は　観察者（Ｄ）に到達する。


この時、Ｂの観察者は、

X’ ＝ α ( X - v t )　＝　α ( d - v d/c ) ;

　 t’ ＝ α ( v X / c | 2 - t )　＝ α ( v t / c - t ) ;


となり、

　　　X’ = α ( 1 - v /c ) d　　；

　 t’ = α ( v / c - 1 ) t　　；


より、　同様に、


　　　　t'/t = - X'/X = sqrt ( ( c - v ) / ( c + v ) ) < 1 ;


を得る。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊




＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

事象（E）の定義

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


観察者（B）の座標系で、観察者（E）は　X' = d' で静止しているとする。

今、観察者（B）の座標系で、　ｔ'＝0 の時、光が原点からＸ'軸正の方向に

出てとする。　X' = d' = ct' ; t' = d'/c で　光は　観察者（E）に到達する。


この時、Aの観察者は、

X ＝ α ( X' - v t' )　＝　α ( d' - v d'/c ) ;

　 t ＝ α ( v X' / c | 2 - t' )　＝ α ( v t '/ c - t' ) ;


となり、

　　　X = α ( 1 - v /c ) d'　　；

　 t = α ( v / c - 1 ) t'　　；


より、　同様に、


　　　　t/t' = - X/X' = sqrt ( ( c - v ) / ( c + v ) ) < 1 ;


を得る。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊



＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

事象（H）の定義

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

観測者 A　 から見て、 観測者 B　 は速度 v で動いているとする。

観測者 B　 から見て、 観測者 A は速度 v で動いているとする。





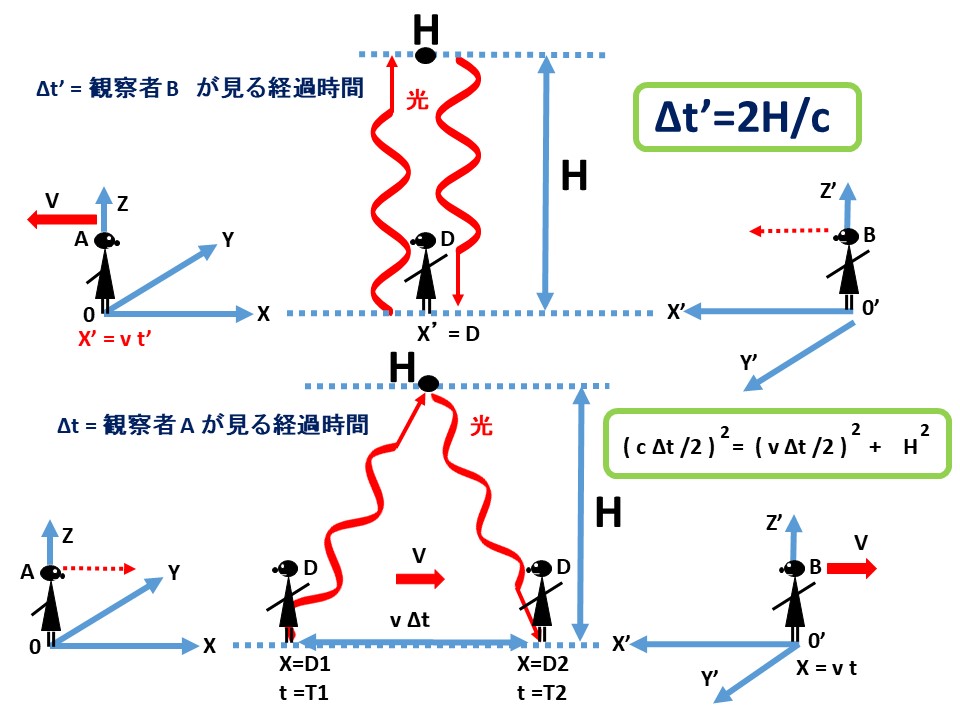
今、観察者 B の座標系において　X’ = D’に静止している D から

頭上 ( Z’ 軸方向） に向かって、光が高さ H まで飛び、さらに。

反射して D’ に戻ってきたとする。


Δt’ = 観察者 Bが見る経過時間とすると、

光が戻ってくるまでの時間は　Δt’=　2H/c　 となる。


この事象(H)を観察者 A の座標系で見る.

観察者(D') は速度 v で 観察者(A) から遠ざかっている。

観察者(D') 　はこの時間 Δt = ( T2 - T1 ) の間に　

ΔX = v Δｔ だけ移動したことになる。　


Ａ が観察する光の飛行した距離は、

X=D1 から 点 ( X=D1+(D2-D1)/2 , Y = H ) で反射し、

X=D2 に戻った距離となる。

その距離は、ΔX = c Δt となる。　


従って ( c Δt /2 ) | 2 = ( v Δt /2 ) | 2 　+ 　H | 2 　　となる。


従って 　Δt = ( 2H/c ) / sqrt ( 1 - ( v/c ) | 2 ) となる。





事象（H）の場合も事象（B）と同様に、


　 Ａ の固有時刻 t に対して、　　Ｂの時刻 ｔ’　は Ａ から見て

　t’ / t = - 1/ α 　= sqrt( 1 - ( v / c ) | 2 ) < 1 ; となり、

Ｂ の時刻 t’ はゆっくり進んでいる ように観察者Ａからは見えます。


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊





＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　 　　　 （3）時間の進む速さ

　　　　　 　　　　　　　　　　　まとめ

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

（１）　観察者（Ａ）から動く観察者（Ｂ）を見た場合、

　　　　t’ / t = - 1/ α 　= sqrt( 1 - ( v / c ) | 2 ) < 1 ; となる。


（2）　観察者（Ｂ）から動く観察者（Ａ）を見た場合、

　　　　t / t' = - 1/ α 　= sqrt( 1 - ( v / c ) | 2 ) < 1 ; となる。


（3）　観察者（Ａ）の前方（Ｘ軸正の方向）に光が進むとき、

　　　　t'/t = - X'/X = sqrt ( ( c - v ) / ( c + v ) ) < 1 ;　 となる。


（4）　観察者（B）の前方（Ｘ'軸正の方向）に光が進むとき、

　　　　t/t' = - X/X' = sqrt ( ( c - v ) / ( c + v ) ) < 1 ;　 となる。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊










＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　 　　　 （４）物体の長さ

　　 　　動いている物体(B)の長さは縮んで見えます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


　　観察者A から見て観測者 B が速度 v で動いているとする。


ΔL = ( 座標系Ａで観察する、動いている車（B）の長さ）　

ΔL' = ( 座標系 Bで静止している車の固有長を観察者Bが測定した値）　



車の先端の座標　( t' = t' , X' = 0 ; ｔ = t , X = - vt ; )

車の後端の座標　( t' = t ', X' = - ΔL' ; t = t , X = - vt +ΔL ; )

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊


車を運転する運転手（Ｂ）からは車の固有の長さ（ΔL' ）は変化しないが、

地上にいる人（Ａ）からは車が進行方向に縮んで ( ΔL ) に 見えます。


ΔL /ΔL' = sqrt ( 1 - ( v /c ) | 2 ) < 1


＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊



　　　　以下　　工事中で～す。



**********************************************

　　　　 人工知能パートナー（ＡＩＰＳ）を支える　　　

　　　 デジタル回路の世界

　　　　
***************************************　　

ISBN 978-4-88359-339-2 C3055

本体 9000円＋税　

Ｂ５サイズ　上製　475ページ　（ハードカバー）

***************************************


　 書籍の出版社の紹介　　

　TEL: 042-765-6460(代) 　　青山社

https://www.seizansha.co.jp/ISBN/ISBN978-4-88359-339-2.html


***************************************


return to http://www.aiplab.com